PSNR and SSIM

Introduction
Image quality can be assessed using objective or subjective methods. In the objective method, image quality assessments are performed by different algorithms that analyze the distortions and degradations introduced in an image. Subjective image quality assessments are a method based on the way in which humans experience or perceive image quality.
Particularily, objective image quality assessments are the most important topic that we are currently focused on in image processing applications. Image Quality analysis consist of two objective IQ metric: Full Reference Image quality Assessment (FR-IQA) and No Reference Image Quality Assessment (NR-IQA).
- FR-IQA: To assess the quality of a test image by comparing it with a reference image
- NR-IQA: To assess the quality of a test image without any reference to the original one
An image quality metric can play a variety of roles in image processing applications: to dynamically monitor and adjust image quality, optimize algorithm and parameter settings of image processing system and to benchmark the image processing system, parameter setting and algorithm.
YCbCr color space
In the following introduction of PSNR and SSIM image quality metric, the images are undergo a pre-processing stage: RGB to YCbCr conversion. The RGB to YCbCr conversion can seperate the luma and chroma component of an image.
- Y luminance component: the brightness of the color.
- Cb chrominance component: the blue component relative to the green.
- Cr chrominance component: the blue component relative to the green.
Why can we get rid of the Green component in this color space? Because Green is the color that our human eyes are most semsitive to, Green is naturally included as part of the Luminance Component!
Besides, studies show that human eyes are way more sensitive to luminance instead of chrominance. YCbCr color space ensures that we can achieve a more appealing representation of scenes and images.
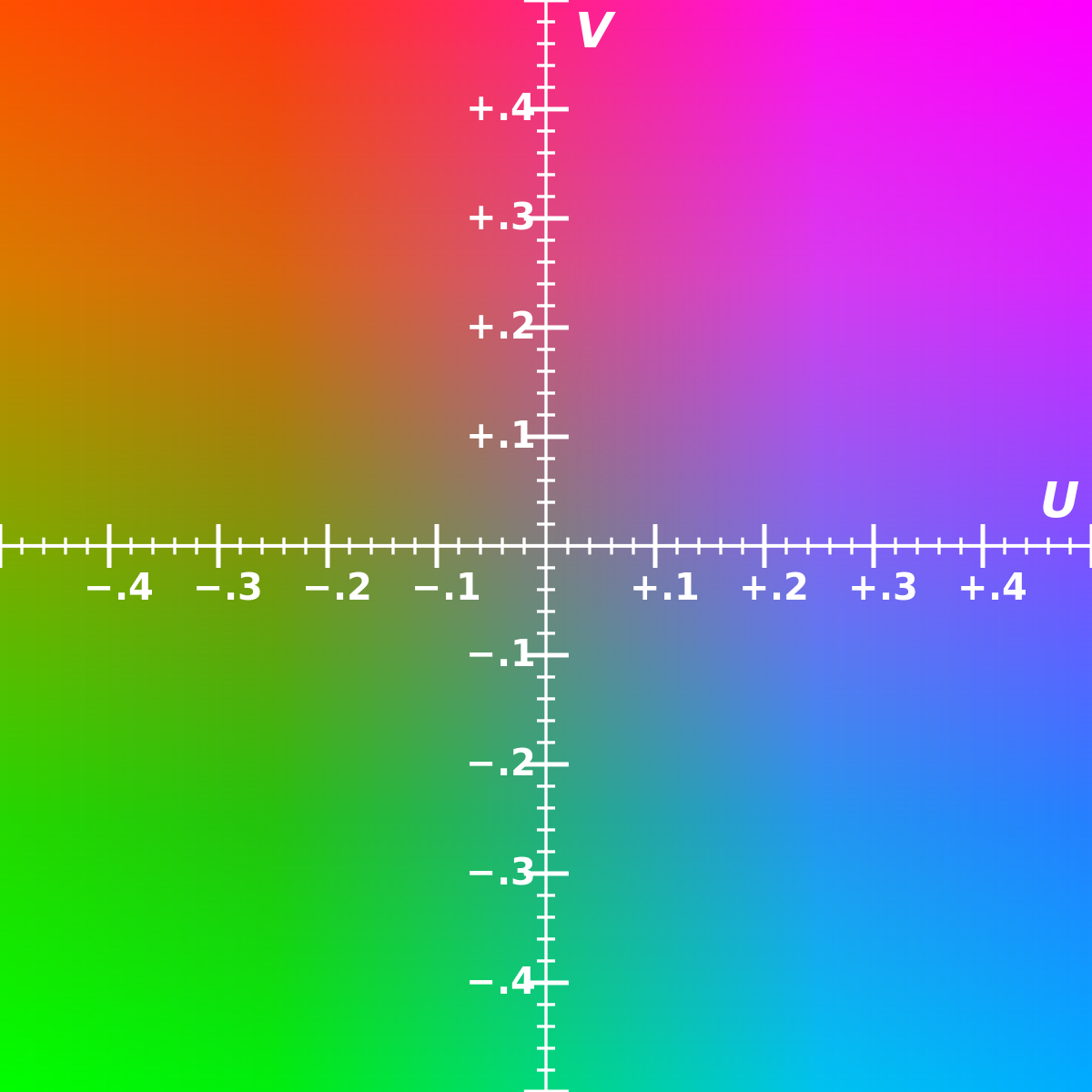
YCbCr is a scaled and offset version of the YUV color space: YUV is an analog system. YCbCr is a digital system. However, they are used interchangeably in the general sense.
PSNR
To measure the difference of the two signals (including images, videos, and vocal signals), Maximal Error, Mean Square Error, Normalized Mean Square Error and Normalized Root Mean Square Error are the most easier measurment method. The idea of PSNR is derived from MSE.
Peak signal-to-noise ratio (PSNR) is the ratio between the maximum possible power of a siganl and the power of corrupting noise that affects the fidelity of its representation. PSNR is usually expressed as a logarithmic quantity using the db scale because many signals have a very wide dynamic range.
PSNR definition
PSNR index is defined by Mean Square Error (MSE). Suppose x[m,n] is the reference image and the y[m,n] is the test image, then MSE is represented by the equation below: $$ MSE = \frac{1}{MN}\sum_{i=0}^{M-1}\sum_{j=0}^{N-1}\left|y[m,n]-x[m,n]\right|^2 $$ Consequently, PSNR is represented by
$$ PSNR = 10·log{_1}{_0}{ \left(\frac{X{_m}{_a}{_x}^2}{MSE}\right)}=20·log{_1}{_0}{ \left(\frac{X{_m}{_a}{_x}}{\sqrt{MSE}}\right)} $$ When the samples are represented with 8 bits per sample, Xmax is 255, the maximum pixel value in the image. More generally, when samples are represented with B bits per sample, Xmax is (2^B)-1 in the formula.
PSNR code
TestImage = imread('test.jpg');
NoiseImage = imnoise(TestImage);
figure; imshow(TestImage);
figure; imshow(NoiseImage);
% if size(image,3) == 1, then the image is gray scale
% convert the image to double-precision array directly
if size(TestImage,3) == 1
y1 = double(TestImage);
y2 = double(NoiseImage);
end
% if size(image,3) == 1, then the image is gray scale
% convert the image from RGB to YCbCr to get luminance
if size(TestImage,3) == 3
TestImage_new = rgb2ycbcr(TestImage);
NoiseImage_new = rgb2ycbcr(NoiseImage);
% the luminance component is in the first array
LuminanceTest = TestImage_new(:,:,1);
LuminanceNoise = NoiseImage_new(:,:,1);
% then convert the image to double-precision array
y1 = double(LuminanceTest);
y2 = double(LuminanceNoise);
end
% the difference of two signals
difference = y2 - y1;
% array(:) convert all the array into a column vector
% array(:) .* array(:) can calculate dot for 2 array
% prod(size(array)) get the sum of array index
MSE = sum( difference(:) .* difference(:)) / prod(size(difference) );
% calculate PSNR, Xmax = 255 in an image
psnr = 10 * log10( 255^2 / MSE )
PSNR disadvantages
However, PSNR index cannot really well matched to the human perceived visual quality. The following images below are Picture 1, Picture 2, and Picture 3, respectively.

Reference: Jian-Jiun Ding, Advanced Digital SIgnal Processing class note, the Department of Electrical Engineering, National Taiwan University (NTU), Taipei, Taiwan.
Logically speaking, Picture 1 and Picture 3 are more similar, but the MSE between Picture 1 and 2 is 0.4411, and the MSE between Picture 1 and 3 is 0.4460. Consequently, PSNR image quality assessment has its limitation.
SSIM
Every pixel of natural image carries important information about the structure of the objects in the visual scenes. The motivation of new approach is to find a more direct way to compare the structures of the “reference image” and the “test image”.
Because the human visual system is highly adapted to extract structure information from the viewing field, Structure Similarity Metric (SSIM) turns out to be an important metric that quantifies image quality compared to a reference image. The similarity measurement is separated into three components: Luminance, Contrast and Structure.
- The luminance is estimated as mean intensity
- The contrast is estimated as standard deviations
- The structure is estimated by normalized standard deviations
SSIM actually measures the perceptual difference between two similar images. It cannot judge which of the two is better, but it can provide some benchmark analysis information (the quality of contrast in the test image compared to the reference).
SSIM definition
SSIM index is calculated between two windows x and y by the following algorithm: $$ SSIM = \left(\frac{2μ{_x}μ{_y}+c{_1}}{ μ{_x}^2+ μ{_y}^2+c{_1}}\right)\left(\frac{2σ{_x}σ{_y}+c{_2}}{σ{_x}^2+σ{_y}^2+c{_2}}\right) $$
- μx, μy: means of x and y / σx, σy: variances of x and y
- σxy: covariance of x and y / c1, c2: adjustable constant parameters
- L: ( the maximal possible value of x ) - ( the minimal possible value if x ) = 255
SSIM component
There are three comparison measuremtent between the reference image (x) and the test image (y) in the SSIM algorithm: Luminance (l), Contrast (c), structure (s): $$ l(x,y) = \frac{2μ{_x}μ{_y}+(c{_1}L)^2}{ μ{_x}^2+ μ{_y}^2+(c{_1}L)^2}, \quad c(x,y) = \frac{2σ{_x}σ{_y}+(c{_2}L)^2}{σ{_x}^2+σ{_y}^2+(c{_2}L)^2}, \quad s(x,y) = \frac{σ{_x}{_y}+(c{_3}L)^2}{σ{_x}σ{_y}+(c{_3}L)^2} $$ SSIM is the weighted combination of these three components, by setting their weights to the same, the SSIM formula the can be simplified to the form shown above.
SSIM code
clear; close all; clc;
ReferenceImage = imread('reference.jpg');
TestImage = imread('test.jpg');
% Set the size of Test Image equal to Reference Image
% ================================================================
TestRow = size(TestImage,1);
TestColumn = size(TestImage,2);
TestRow_modified = size(ReferenceImage, 1);
TestColumn_modified = size(ReferenceImage, 2);
% Create (x,y) pairs for each point in the image and define its coordinate
% X-axis: the number of column / Y-axis: the number of row
% [ column, row ] = meshgrid( 1 : column, 1 : row )
[n1, m1] = meshgrid(1 : TestColumn_modified, 1 : TestRow_modified);
% Let Sm = m / m' and let m = m' * Sm for m = 1,...,m'
Sm = TestRow / TestRow_modified; m1 = m1 * Sm;
% Let Sn = n / n' Let nf = c' * Sn for n = 1,...,n'
Sn = TestColumn / TestColumn_modified; n1 = n1 * Sn;
% Let m = round(m1) and n = round(n1)
m = round(m1);
n = round(n1);
% Setting the values out of range
m(m < 1) = 1;
n(n < 1) = 1;
m(m > TestRow - 1) = TestRow - 1;
n(n > TestColumn - 1) = TestColumn - 1;
% Setting delta_m = m1 - m, delta_n = n1 - n
delta_m = m1 - m;
delta_n = n1 - n;
% Get indices for each point we wish to access
Test1_index = sub2ind([TestRow, TestColumn], m, n);
Test2_index = sub2ind([TestRow, TestColumn], m+1, n);
Test3_index = sub2ind([TestRow, TestColumn], m, n+1);
Test4_index = sub2ind([TestRow, TestColumn], m+1, n+1);
% Interpolate: Go through each channel for the case of colour
% Create output image that is the same class as input
ModifiedTestImage = zeros(TestRow_modified, TestColumn_modified, size(TestImage, 3));
ModifiedTestImage = cast(ModifiedTestImage, class(TestImage));
for index = 1 : size(TestImage, 3)
% Get i'th channel to get its color matrix
channel = double(TestImage(:,:,index));
% Interpolate the channel
tmp = channel(Test1_index) .* (1 - delta_m) .* (1 - delta_n) + ...
channel(Test2_index) .* (delta_m) .* (1 - delta_n) + ...
channel(Test3_index) .* (1 - delta_m) .* (delta_n) + ...
channel(Test4_index) .* (delta_m) .* (delta_n);
ModifiedTestImage(:,:,index) = cast(tmp, class(TestImage));
end
% Implement the algorithm of SSIM
% ===============================================================
c1 = input('c1: '); % recommand: c1 = 0.01
c2 = input('c2: '); % recommand: c2 = 0.03
% if size(image,3) == 1, then the image is gray scale
% convert the image to double-precision array directly
if size(ReferenceImage,3) == 1
x = double(ReferenceImage);
end
if size(ModifiedTestImage,3) == 1
y = double(ModifiedTestImage);
end
% if size(image,3) == 1, then the image is gray scale
% convert the image from RGB to YCbCr to get luminance
if size(ReferenceImage,3) == 3
ReferenceImage_new = rgb2ycbcr(ReferenceImage);
% the luminance component is in the first array
LuminanceReference = ReferenceImage_new(:,:,1);
% then convert the image to double-precision array
x = double(LuminanceReference);
end
if size(ModifiedTestImage,3) == 3
TestImage_new = rgb2ycbcr(ModifiedTestImage);
% the luminance component is in the first array
LuminanceTest = TestImage_new(:,:,1);
% then convert the image to double-precision array
y = double(LuminanceTest);
end
mean_x = sum(sqrt( x(:).*x(:) )) / prod(size(x));
mean_y = sum(sqrt( y(:).*y(:) )) / prod(size(y));
Xdiff = x - mean_x;
variance_x = sqrt( sum( Xdiff(:).*Xdiff(:) ) / prod(size(x) ) );
Ydiff = y - mean_y;
variance_y = sqrt( sum( Ydiff(:).*Ydiff(:) ) / prod(size(y) ) );
variance_xy = sum( Xdiff(:).*Ydiff(:) ) / prod(size(x) );
L = 255;
Component1 = ( 2*mean_x*mean_y + (c1*L)^2 ) / ( mean_x^2+mean_y^2 + (c1*L)^2 );
Component2 = ( 2*variance_xy + (c2*L)^2 ) / ( variance_x^2 + variance_y^2 + (c2*L)^2 );
imshow(ReferenceImage)
imshow(ModifiedTestImage)
luminance_component = ( 2*mean_x*mean_y + (c1*L)^2 ) / ( mean_x^2+mean_y^2 + (c1*L)^2 )
contrast_component = ( 2*variance_xy + (c2*L)^2 ) / ( variance_x^2 + variance_y^2 + (c2*L)^2 )
SSIM = Component1*Component2
Benchmark Analysis
Here are 8 pictures photographed using the same scene. Each picture has the same luminance and structure but different contrast information. By setting luminance and structure parameters of the reference and the test image to an approximate identity, we can use the SSIM index to objectively compare the contrast quality between them.
 contrast+80 (image 1)
contrast+80 (image 1)
 contrast+60 (image 2)
contrast+60 (image 2)
 contrast+40 (image 3)
contrast+40 (image 3)
 contrast+20 (image 4)
contrast+20 (image 4)
 contrast 0 (image 5)
contrast 0 (image 5)
 contrast-20 (image 6)
contrast-20 (image 6)
 contrast-40 (image 7)
contrast-40 (image 7)
 contrast-60 (image 8)
contrast-60 (image 8)
 contrast-60 (image 9)
contrast-60 (image 9)
Benchmark Analysis Result
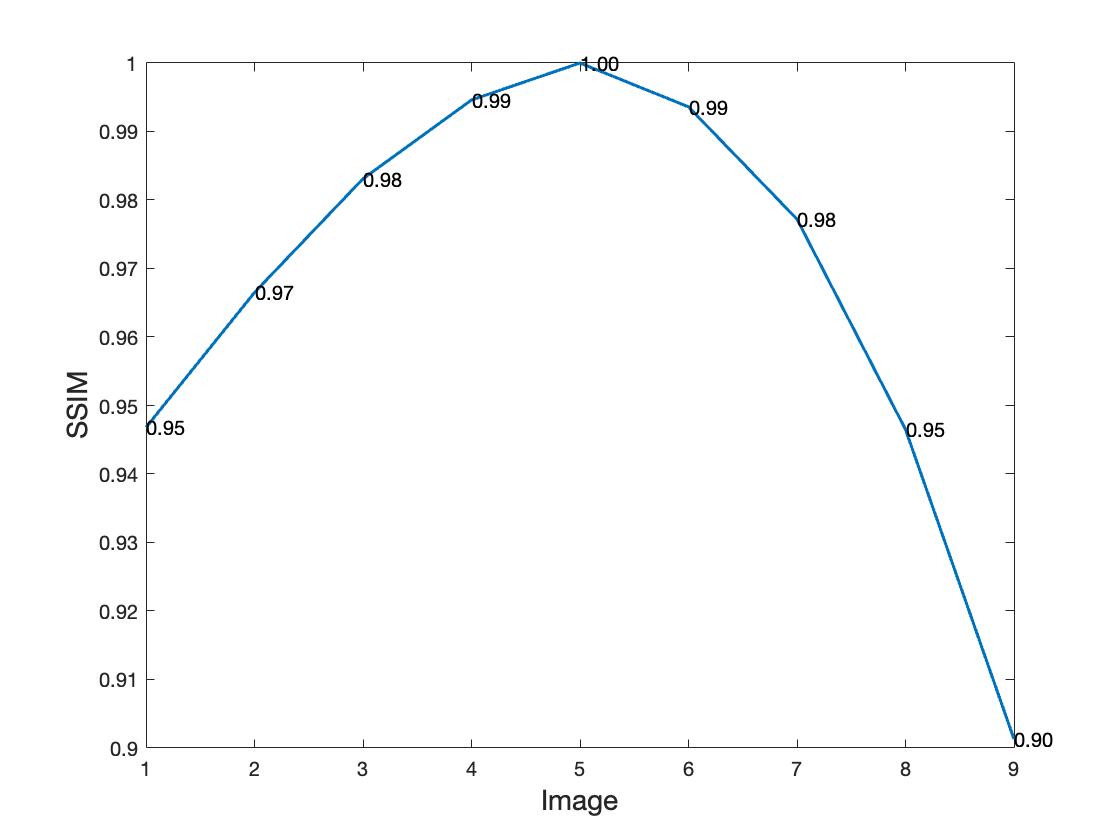
Because “image 5” (contrast 0) seems like the picture with the greatest contrast for our human visual system, let’s take “image 5” (contrast 0) as the reference image for this SSIM benchmark analysis.
In order to rank each picture’s contrast quality, this project is assessed and benchmarked by SSIM index.
| 1 vs 5 | 2 vs 5 | 3 vs 5 | 4 vs 5 | 6 vs 5 | 7 vs 5 | 8 vs 5 | 9 vs 5 | |
|---|---|---|---|---|---|---|---|---|
| l(x,y) | 0.9995 | 0.9997 | 0.9998 | 1.0000 | 1.0000 | 0.9999 | 0.9997 | 0.9996 |
| c(x,y) | 0.9473 | 0.9669 | 0.9832 | 0.9946 | 0.9937 | 0.9773 | 0.9468 | 0.9017 |
| SSIM | 0.9468 | 0.9665 | 0.9831 | 0.9946 | 0.9936 | 0.9772 | 0.9465 | 0.9013 |
Based on the data shown above, we can assume that the contrast quality ranking, from good to bad, becomes image 4, 6, 3, 7, 2, 1, 8, 5.
SSIM disadvantages
SSIM is limited when the images has unstructured distortion. It is sensitive to image rotations and image translations. If we are using SSIM index for competitor analysis and trying to compare images where both camera’s FOV (field of view) are slightly different, then it’ll leads to erroneous image quality measurements.