Professional image qualuty analysis softwares such as Imatest and iQ-analyzer provide objective, comprehensive, and consistent evaluations of camera image quality. In our practical experience, we have observed that different software employs varying algorithms for calculating the color difference. To enable efficient automated image analysis, we conducted extensive experimental studies to uncover the color difference algorithms employed by various softwares. This work will discuss the advantages, disadvantages, and implementation specifics of the two algorithms.

Introduction

The ColorChecker® Patch Classic target is an array of 24 scientifically prepared natural, chromatic, primary and grayscale colored squares. These calibrated patches cover a broad spectrum of colors. When included in a test image, the ColorChecker serves as a reliable reference for comparing the captured output of cameras to the original chart’s accurate color measurements, ensuring precise color reproduction and consistency.

Figure 1. The ground-truth RGB pixel values for each color patch in the The ColorChecker®.

ColorChecker Application

1. Provides a standard for camera calibration in image color accuracy and auto white balance.
2. Enables an accurate calculation of ΔE* and ΔC* to quantify the image color difference.

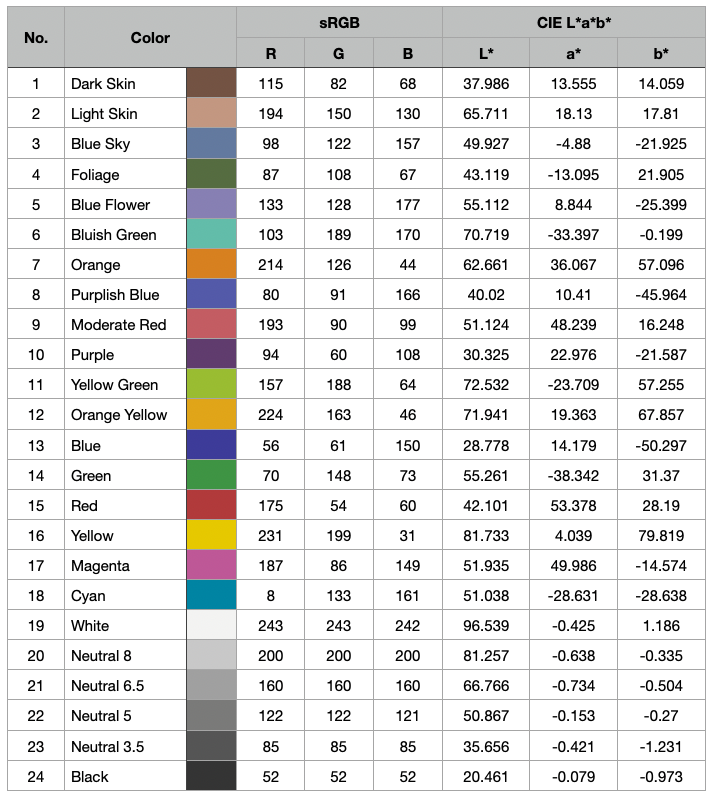
Figure 2. CIELAB values in illuminate D50 for The ColorChecker® Patch Classic

Color & Chroma Difference

Calculating the color and chroma difference of images with the ColorChecker serves as a quantitative measure of a camera’s color reproduction accuracy.

The CIE Lab color space was specifically designed to model human vision and is widely ised for calculating color differences due to the perceptual uniformity: equal distances in the Lab space correspond to equal perceived color differences. In the Lab color space, L*, a*, and b* are represented as the luminance, the color on a green-red scale, and the color on a blue-uellow scale.

1. The CIE 1976 standard

The absolute difference of color ΔE* and chroma ΔC* are calculated by measuring the Eucliean distance of two Lab coordinates. Compared to the ΔE formula, the chroma difference ΔC is calculated without considering luminance for better focusing on the color inaccuracies independently of camera exposure error.

$$ ΔE_{ab}^* = \sqrt{(L_2^* - L_1^*)^2 + (a_2^* - a_1^*)^2 + (b_2^* - b_1^*)^2} $$

$$ ΔC_{ab}^*=\sqrt{(a_2^*-a_1^*)^2+(b_2^*-b_1^*)^2}=\sqrt{(ΔE^*)^2+(L_2^*-L_1^*)^2} $$

2. The CIE 2000 standard

The formulas of ΔE* and ΔC* are revised to better address the perceptual non-uniformity problem. The CIE 2000 standard introuduced two major improvements in the color difference calculation:

1. using new color space LCh model instead of Lab model.
2. adding a weighting factor to balance lightness, chroma, and hue components.
3. including a rotational term to account for interactions between chroma and hue.

The CIE LCh color model is an alternative representation of Lab coordinates. In the LCh color space, L*, C*, and h* are represented as the luminance, chroma (the saturation of the color), and hue (hue angle from 0° to 360° represent the color’s type). Chroma is calculated by the Eucliean distance from the center (neutral gray), and hue angle is calculated by h = arctan( b/a ). The comprehensive calculation of the color difference in CIE 2000 standard can be found in [here].

3. Industrial Color Difference Algorithm

The first step in calculating ΔE* and ΔC* involves converting the RGB color space to the Lab color space, which requires an intermediate transformation to the XYZ color space. As the source and target color spaces may have different reference white points, chromatic adaptation is necessary to ensure an accurate conversion.

Since the Lab reference white point of both Imatest and IQ-analyer is D50 and the RGB2XYZ transformation matrix is based on D65 illumination, the D50 chroma adaption needs to be applied in the calculation. However, in our experiments, we found that Imatest ignore the D50 Chorma Adaption in its color difference calculation.

Denoted M1 as the RGB2XYZ transformation matrix and M2 as the Bradford matrix used for chroma adaption. The overall Lab conversion flowchart of Imatest and iQ-analyzer are shown below. $$ M_1 = \begin{bmatrix} 0.4124564 & 0.3575761 & 0.1804375 \\ 0.2126729 & 0.7151522 & 0.0721750 \\ 0.0193339 & 0.1191920 & 0.9503041 \end{bmatrix} $$

$$ M_2 = \begin{bmatrix} 1.0478112 & 0.0228866 & -0.050127 \\ 0.0295424 & 0.9904844 & -0.017049 \\ -0.009234 & 0.0150436 & 0.7521316 \end{bmatrix} $$

1. Imatest: sRGB ➝ D65XYZ (M1) ➝ Lab
2. iQ-analyzer: sRGB ➝ D65XYZ (M1) ➝ D50XYZ (M2) ➝ Lab

Figure 3. Overall Lab conversion flowchart. Reference: [Paper]

In our research, we revealed that the chroma coordinates of Imatest and iQ-analyzer’s algorithms are different,

1. Imatest: The chroma difference calculated by Imatest is shown below, which is represented in the rectangular coordinate. $$ ΔC_{ab}^*=\sqrt{(a_2^*-a_1^*)^2+(b_2^*-b_1^*)^2} $$

$$ ΔC_{00}^*= ΔE_{00}^* \ \ without \ \ \left( \frac{\Delta L’}{K_L S_L} \right)^2 $$

2. iQ-analyzer: The chroma difference calculated by iQ-analyzer is shown below, which is represented in the polar coordinate. $$ ΔC_{ab}^*= \sqrt{(a_2^*+a_1^*)^2} - \sqrt{(b_2^*+b_1^*)^2} $$

$$ ΔC_{00}^*= \frac{\Delta C’}{K_C S_C} $$

The difference of chroma coordinates is the main reason why the chroma difference calculated by iQ-Analyzer may have negative values.

Notes

This study represents the findings and results of a collaborative effort conducted with Allen Tsou in 2023.

Reference

1. ColorChecker reference table: https://xritephoto.com/documents/literature/en/ColorData-1p_EN.pdf
2. Imatest ColorChecker application: https://www.imatest.com/support/docs/22-1/colorcheck_ref/
3. iQ-analyzer ColorChecker application: https://www.image-engineering.de/news/product-news/773-the-iq-analyzer-color-bundle
4. The CIEDE2000 Color-Difference Formula: Implementation Notes, Supplementary Test Data, and Mathematical Observations: https://hajim.rochester.edu/ece/sites/gsharma/ciede2000/ciede2000noteCRNA.pdf